字符集和字符编码（Charset & Encoding）

来源: 吴秦 原文链接

---

——每个软件开发人员应该无条件掌握的知识！
——Unicode伟大的创想！
相信大家一定碰到过，打开某个网页，却显示一堆像乱码，如"бЇЯАзЪСЯ"、"�????????"？还记得HTTP中的Accept-Charset、Accept-Encoding、Accept-Language、Content-Encoding、Content-Language等消息头字段？这些就是接下来我们要探讨的。
目录：

• 1.基础知识
• 2.常用字符集和字符编码
  • 2.1. ASCII字符集&编码
  • 2.2. GBXXXX字符集&编码
  • 2.3. BIG5字符集&编码
• 3.伟大的创想Unicode
  • 3.1.UCS & UNICODE
  • 3.2.UTF-32
  • 3.3.UTF-16
  • 3.4.UTF-8
• 4.Accept-Charset/Accept-Encoding/Accept-Language/Content-Type/Content-Encoding/Content-Language
• 参考文献&进一步阅读

1.基础知识

计算机中储存的信息都是用二进制数表示的；而我们在屏幕上看到的英文、汉字等字符是二进制数转换之后的结果。通俗的说，按照何种规则将字符存储在计算机中，如'a'用什么表示，称为"编码"；反之，将存储在计算机中的二进制数解析显示出来，称为"解码"，如同密码学中的加密和解密。在解码过程中，如果使用了错误的解码规则，则导致'a'解析成'b'或者乱码。
字符集（Charset）：是一个系统支持的所有抽象字符的集合。字符是各种文字和符号的总称，包括各国家文字、标点符号、图形符号、数字等。
字符编码（Character Encoding）：是一套法则，使用该法则能够对自然语言的字符的一个集合（如字母表或音节表），与其他东西的一个集合（如号码或电脉冲）进行配对。即在符号集合与数字系统之间建立对应关系，它是信息处理的一项基本技术。通常人们用符号集合（一般情况下就是文字）来表达信息。而以计算机为基础的信息处理系统则是利用元件（硬件）不同状态的组合来存储和处理信息的。元件不同状态的组合能代表数字系统的数字，因此字符编码就是将符号转换为计算机可以接受的数字系统的数，称为数字代码。

2.常用字符集和字符编码

常见字符集名称：ASCII字符集、GB2312字符集、BIG5字符集、GB18030字符集、Unicode字符集等。计算机要准确的处理各种字符集文字，需要进行字符编码，以便计算机能够识别和存储各种文字。

2.1. ASCII字符集&编码

ASCII（American Standard Code for Information Interchange，美国信息交换标准代码）是基于拉丁字母的一套电脑编码系统。它主要用于显示现代英语，而其扩展版本EASCII则可以勉强显示其他西欧语言。它是现今最通用的单字节编码系统（但是有被Unicode追上的迹象），并等同于国际标准ISO/IEC 646。
ASCII字符集：主要包括控制字符（回车键、退格、换行键等）；可显示字符（英文大小写字符、阿拉伯数字和西文符号）。
ASCII编码：将ASCII字符集转换为计算机可以接受的数字系统的数的规则。使用7位（bits）表示一个字符，共128字符；但是7位编码的字符集只能支持128个字符，为了表示更多的欧洲常用字符对ASCII进行了扩展，ASCII扩展字符集使用8位（bits）表示一个字符，共256字符。ASCII字符集映射到数字编码规则如下图所示：

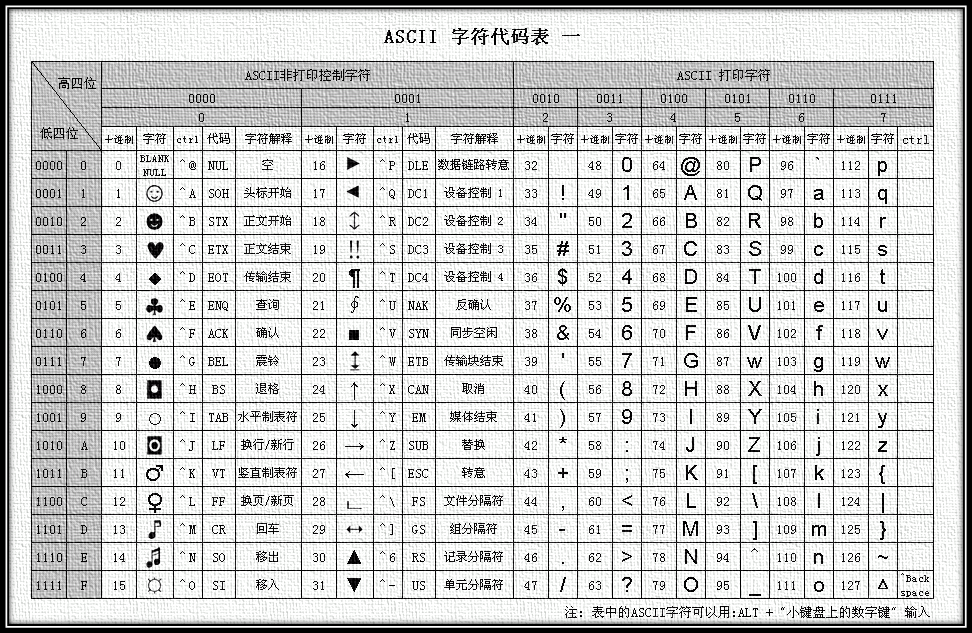
图1 ASCII编码表

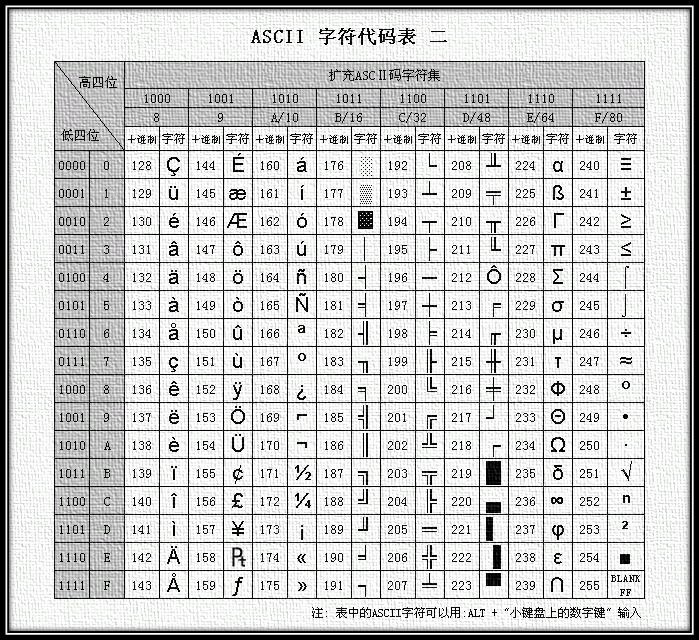
图2 扩展ASCII编码表
ASCII的最大缺点是只能显示26个基本拉丁字母、阿拉伯数目字和英式标点符号，因此只能用于显示现代美国英语（而且在处理英语当中的外来词如naïve、café、élite等等时，所有重音符号都不得不去掉，即使这样做会违反拼写规则）。而EASCII虽然解决了部份西欧语言的显示问题，但对更多其他语言依然无能为力。因此现在的苹果电脑已经抛弃ASCII而转用Unicode。

2.2. GBXXXX字符集&编码

计算机发明之处及后面很长一段时间，只用应用于美国及西方一些发达国家，ASCII能够很好满足用户的需求。但是当天朝也有了计算机之后，为了显示中文，必须设计一套编码规则用于将汉字转换为计算机可以接受的数字系统的数。
天朝专家把那些127号之后的奇异符号们（即EASCII）取消掉，规定：一个小于127的字符的意义与原来相同，但两个大于127的字符连在一起时，就表示一个汉字，前面的一个字节（他称之为高字节）从0xA1用到 0xF7，后面一个字节（低字节）从0xA1到0xFE，这样我们就可以组合出大约7000多个简体汉字了。在这些编码里，还把数学符号、罗马希腊的 字母、日文的假名们都编进去了，连在ASCII里本来就有的数字、标点、字母都统统重新编了两个字节长的编码，这就是常说的"全角"字符，而原来在127号以下的那些就叫"半角"字符了。
上述编码规则就是GB2312。GB2312或GB2312-80是中国国家标准简体中文字符集，全称《信息交换用汉字编码字符集·基本集》，又称GB0，由中国国家标准总局发布，1981年5月1日实施。GB2312编码通行于中国大陆；新加坡等地也采用此编码。中国大陆几乎所有的中文系统和国际化的软件都支持GB2312。GB2312的出现，基本满足了汉字的计算机处理需要，它所收录的汉字已经覆盖中国大陆99.75%的使用频率。对于人名、古汉语等方面出现的罕用字，GB2312不能处理，这导致了后来GBK及GB 18030汉字字符集的出现。下图是GB2312编码的开始部分（由于其非常庞大，只列举开始部分，具体可查看GB2312简体中文编码表）：

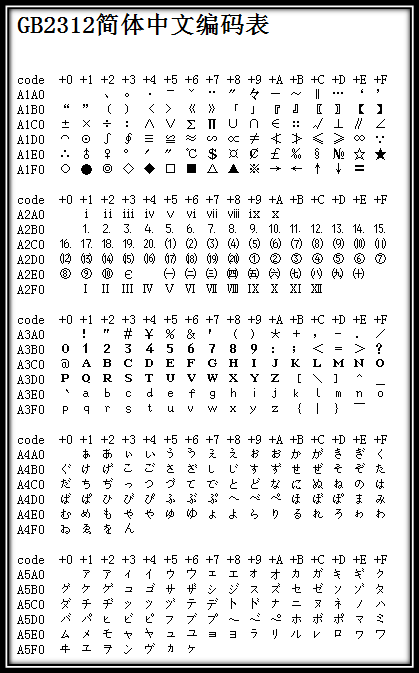
图3 GB2312编码表的开始部分
由于GB 2312-80只收录6763个汉字，有不少汉字，如部分在GB 2312-80推出以后才简化的汉字（如"啰"），部分人名用字（如中国前总理朱镕基的"镕"字），台湾及香港使用的繁体字，日语及朝鲜语汉字等，并未有收录在内。于是厂商微软利用GB 2312-80未使用的编码空间，收录GB 13000.1-93全部字符制定了GBK编码。根据微软资料，GBK是对GB2312-80的扩展，也就是CP936字码表 (Code Page 936)的扩展（之前CP936和GB 2312-80一模一样），最早实现于Windows 95简体中文版。虽然GBK收录GB 13000.1-93的全部字符，但编码方式并不相同。GBK自身并非国家标准，只是曾由国家技术监督局标准化司、电子工业部科技与质量监督司公布为"技术规范指导性文件"。原始GB13000一直未被业界采用，后续国家标准GB18030技术上兼容GBK而非GB13000。
GB 18030，全称：国家标准GB 18030-2005《信息技术 中文编码字符集》，是中华人民共和国现时最新的内码字集，是GB 18030-2000《信息技术 信息交换用汉字编码字符集 基本集的扩充》的修订版。与GB 2312-1980完全兼容，与GBK基本兼容，支持GB 13000及Unicode的全部统一汉字，共收录汉字70244个。GB 18030主要有以下特点：

• 与UTF-8相同，采用多字节编码，每个字可以由1个、2个或4个字节组成。
• 编码空间庞大，最多可定义161万个字符。
• 支持中国国内少数民族的文字，不需要动用造字区。
• 汉字收录范围包含繁体汉字以及日韩汉字
  
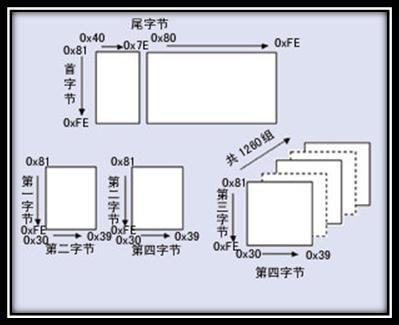
  图4 GB18030编码总体结构
  本规格的初版使中华人民共和国信息产业部电子工业标准化研究所起草，由国家质量技术监督局于2000年3月17日发布。现行版本为国家质量监督检验总局和中国国家标准化管理委员会于2005年11月8日发布，2006年5月1日实施。此规格为在中国境内所有软件产品支持的强制规格。
  
  

  2.3. BIG5字符集&编码

  Big5，又称为大五码或五大码，是使用繁体中文（正体中文）社区中最常用的电脑汉字字符集标准，共收录13,060个汉字。中文码分为内码及交换码两类，Big5属中文内码，知名的中文交换码有CCCII、CNS11643。Big5虽普及于台湾、香港与澳门等繁体中文通行区，但长期以来并非当地的国家标准，而只是业界标准。倚天中文系统、Windows等主要系统的字符集都是以Big5为基准，但厂商又各自增加不同的造字与造字区，派生成多种不同版本。2003年，Big5被收录到CNS11643中文标准交换码的附录当中，取得了较正式的地位。这个最新版本被称为Big5-2003。
  Big5码是一套双字节字符集，使用了双八码存储方法，以两个字节来安放一个字。第一个字节称为"高位字节"，第二个字节称为"低位字节"。"高位字节"使用了0x81-0xFE，"低位字节"使用了0x40-0x7E，及0xA1-0xFE。在Big5的分区中：
  

  0x8140-0xA0FE	保留给用户自定义字符（造字区）
  0xA140-0xA3BF	标点符号、希腊字母及特殊符号，包括在0xA259-0xA261，安放了九个计量用汉字：兙兛兞兝兡兣嗧瓩糎。
  0xA3C0-0xA3FE	保留。此区没有开放作造字区用。
  0xA440-0xC67E	常用汉字，先按笔划再按部首排序。
  0xC6A1-0xC8FE	保留给用户自定义字符（造字区）
  0xC940-0xF9D5	次常用汉字，亦是先按笔划再按部首排序。
  0xF9D6-0xFEFE	保留给用户自定义字符（造字区）

  Unicode字符集&UTF编码
  
  

  3.伟大的创想Unicode

  ——不得不单独说Unicode
  像天朝一样，当计算机传到世界各个国家时，为了适合当地语言和字符，设计和实现类似GB232/GBK/GB18030/BIG5的编码方案。这样各搞一套，在本地使用没有问题，一旦出现在网络中，由于不兼容，互相访问就出现了乱码现象。
  为了解决这个问题，一个伟大的创想产生了——Unicode。Unicode编码系统为表达任意语言的任意字符而设计。它使用4字节的数字来表达每个字母、符号，或者表意文字(ideograph)。每个数字代表唯一的至少在某种语言中使用的符号。（并不是所有的数字都用上了，但是总数已经超过了65535，所以2个字节的数字是不够用的。）被几种语言共用的字符通常使用相同的数字来编码，除非存在一个在理的语源学(etymological)理由使不这样做。不考虑这种情况的话，每个字符对应一个数字，每个数字对应一个字符。即不存在二义性。不再需要记录"模式"了。U+0041总是代表'A'，即使这种语言没有'A'这个字符。
  在计算机科学领域中，Unicode（统一码、万国码、单一码、标准万国码）是业界的一种标准，它可以使电脑得以体现世界上数十种文字的系统。Unicode 是基于通用字符集（Universal Character Set）的标准来发展，并且同时也以书本的形式^[1]对外发表。Unicode 还不断在扩增， 每个新版本插入更多新的字符。直至目前为止的第六版，Unicode 就已经包含了超过十万个字符（在2005年，Unicode 的第十万个字符被采纳且认可成为标准之一）、一组可用以作为视觉参考的代码图表、一套编码方法与一组标准字符编码、一套包含了上标字、下标字等字符特性的枚举等。Unicode 组织（The Unicode Consortium）是由一个非营利性的机构所运作，并主导 Unicode 的后续发展，其目标在于：将既有的字符编码方案以Unicode 编码方案来加以取代，特别是既有的方案在多语环境下，皆仅有有限的空间以及不兼容的问题。
  （可以这样理解：Unicode是字符集，UTF-32/ UTF-16/ UTF-8是三种字符编码方案。）
  
  

  3.1.UCS & UNICODE

  通用字符集（Universal Character Set，UCS）是由ISO制定的ISO 10646（或称ISO/IEC 10646）标准所定义的标准字符集。历史上存在两个独立的尝试创立单一字符集的组织，即国际标准化组织（ISO）和多语言软件制造商组成的统一码联盟。前者开发的 ISO/IEC 10646 项目，后者开发的统一码项目。因此最初制定了不同的标准。
  1991年前后，两个项目的参与者都认识到，世界不需要两个不兼容的字符集。于是，它们开始合并双方的工作成果，并为创立一个单一编码表而协同工作。从Unicode 2.0开始，Unicode采用了与ISO 10646-1相同的字库和字码；ISO也承诺，ISO 10646将不会替超出U+10FFFF的UCS-4编码赋值，以使得两者保持一致。两个项目仍都存在，并独立地公布各自的标准。但统一码联盟和ISO/IEC JTC1/SC2都同意保持两者标准的码表兼容，并紧密地共同调整任何未来的扩展。在发布的时候，Unicode一般都会采用有关字码最常见的字型，但ISO 10646一般都尽可能采用Century字型。
  
  

  3.2.UTF-32

  上述使用4字节的数字来表达每个字母、符号，或者表意文字(ideograph)，每个数字代表唯一的至少在某种语言中使用的符号的编码方案，称为UTF-32。UTF-32又称UCS-4是一种将Unicode字符编码的协定，对每个字符都使用4字节。就空间而言，是非常没有效率的。
  这种方法有其优点，最重要的一点就是可以在常数时间内定位字符串里的第N个字符，因为第N个字符从第4×Nth个字节开始。虽然每一个码位使用固定长定的字节看似方便，它并不如其它Unicode编码使用得广泛。
  
  

  3.3.UTF-16

  尽管有Unicode字符非常多，但是实际上大多数人不会用到超过前65535个以外的字符。因此，就有了另外一种Unicode编码方式，叫做UTF-16(因为16位 = 2字节)。UTF-16将0–65535范围内的字符编码成2个字节，如果真的需要表达那些很少使用的"星芒层(astral plane)"内超过这65535范围的Unicode字符，则需要使用一些诡异的技巧来实现。UTF-16编码最明显的优点是它在空间效率上比UTF-32高两倍，因为每个字符只需要2个字节来存储（除去65535范围以外的），而不是UTF-32中的4个字节。并且，如果我们假设某个字符串不包含任何星芒层中的字符，那么我们依然可以在常数时间内找到其中的第N个字符，直到它不成立为止这总是一个不错的推断。其编码方法是：
• 如果字符编码U小于0x10000，也就是十进制的0到65535之内，则直接使用两字节表示；
• 如果字符编码U大于0x10000，由于UNICODE编码范围最大为0x10FFFF，从0x10000到0x10FFFF之间 共有0xFFFFF个编码，也就是需要20个bit就可以标示这些编码。用U'表示从0-0xFFFFF之间的值，将其前 10 bit作为高位和16 bit的数值0xD800进行 逻辑or 操作，将后10 bit作为低位和0xDC00做 逻辑or 操作，这样组成的 4个byte就构成了U的编码。
  对于UTF-32和UTF-16编码方式还有一些其他不明显的缺点。不同的计算机系统会以不同的顺序保存字节。这意味着字符U+4E2D在UTF-16编码方式下可能被保存为4E 2D或者2D 4E，这取决于该系统使用的是大尾端(big-endian)还是小尾端(little-endian)。（对于UTF-32编码方式，则有更多种可能的字节排列。）只要文档没有离开你的计算机，它还是安全的——同一台电脑上的不同程序使用相同的字节顺序(byte order)。但是当我们需要在系统之间传输这个文档的时候，也许在万维网中，我们就需要一种方法来指示当前我们的字节是怎样存储的。不然的话，接收文档的计算机就无法知道这两个字节4E 2D表达的到底是U+4E2D还是U+2D4E。
  为了解决这个问题，多字节的Unicode编码方式定义了一个"字节顺序标记(Byte Order Mark)"，它是一个特殊的非打印字符，你可以把它包含在文档的开头来指示你所使用的字节顺序。对于UTF-16，字节顺序标记是U+FEFF。如果收到一个以字节FF FE开头的UTF-16编码的文档，你就能确定它的字节顺序是单向的(one way)的了；如果它以FE FF开头，则可以确定字节顺序反向了。
  
  

  3.4.UTF-8

  UTF-8（8-bit Unicode Transformation Format）是一种针对Unicode的可变长度字符编码（定长码），也是一种前缀码。它可以用来表示Unicode标准中的任何字符，且其编码中的第一个字节仍与ASCII兼容，这使得原来处理ASCII字符的软件无须或只须做少部份修改，即可继续使用。因此，它逐渐成为电子邮件、网页及其他存储或传送文字的应用中，优先采用的编码。互联网工程工作小组（IETF）要求所有互联网协议都必须支持UTF-8编码。
  UTF-8使用一至四个字节为每个字符编码：

1. 128个US-ASCII字符只需一个字节编码（Unicode范围由U+0000至U+007F）。
2. 带有附加符号的拉丁文、希腊文、西里尔字母、亚美尼亚语、希伯来文、阿拉伯文、叙利亚文及它拿字母则需要二个字节编码（Unicode范围由U+0080至U+07FF）。
3. 其他基本多文种平面（BMP）中的字符（这包含了大部分常用字）使用三个字节编码。
4. 其他极少使用的Unicode辅助平面的字符使用四字节编码。
   在处理经常会用到的ASCII字符方面非常有效。在处理扩展的拉丁字符集方面也不比UTF-16差。对于中文字符来说，比UTF-32要好。同时，（在这一条上你得相信我，因为我不打算给你展示它的数学原理。）由位操作的天性使然，使用UTF-8不再存在字节顺序的问题了。一份以utf-8编码的文档在不同的计算机之间是一样的比特流。
   总体来说，在Unicode字符串中不可能由码点数量决定显示它所需要的长度，或者显示字符串之后在文本缓冲区中光标应该放置的位置；组合字符、变宽字体、不可打印字符和从右至左的文字都是其归因。所以尽管在UTF-8字符串中字符数量与码点数量的关系比UTF-32更为复杂，在实际中很少会遇到有不同的情形。
   优点

• UTF-8是ASCII的一个超集。因为一个纯ASCII字符串也是一个合法的UTF-8字符串，所以现存的ASCII文本不需要转换。为传统的扩展ASCII字符集设计的软件通常可以不经修改或很少修改就能与UTF-8一起使用。
• 使用标准的面向字节的排序例程对UTF-8排序将产生与基于Unicode代码点排序相同的结果。（尽管这只有有限的有用性，因为在任何特定语言或文化下都不太可能有仍可接受的文字排列顺序。）
• UTF-8和UTF-16都是可扩展标记语言文档的标准编码。所有其它编码都必须通过显式或文本声明来指定。
• 任何面向字节的字符串搜索算法都可以用于UTF-8的数据（只要输入仅由完整的UTF-8字符组成）。但是，对于包含字符记数的正则表达式或其它结构必须小心。
• UTF-8字符串可以由一个简单的算法可靠地识别出来。就是，一个字符串在任何其它编码中表现为合法的UTF-8的可能性很低，并随字符串长度增长而减小。举例说，字符值C0,C1,F5至FF从来没有出现。为了更好的可靠性，可以使用正则表达式来统计非法过长和替代值（可以查看W3 FAQ: Multilingual Forms上的验证UTF-8字符串的正则表达式）。
  缺点
  因为每个字符使用不同数量的字节编码，所以寻找串中第N个字符是一个O(N)复杂度的操作 — 即，串越长，则需要更多的时间来定位特定的字符。同时，还需要位变换来把字符编码成字节，把字节解码成字符。
  
  

  4.Accept-Charset/Accept-Encoding/Accept-Language/Content-Type/Content-Encoding/Content-Language

  在HTTP中，与字符集和字符编码相关的消息头是Accept-Charset/Content-Type，另外主区区分Accept-Charset/Accept-Encoding/Accept-Language/Content-Type/Content-Encoding/Content-Language：
  Accept-Charset：浏览器申明自己接收的字符集，这就是本文前面介绍的各种字符集和字符编码，如gb2312，utf-8（通常我们说Charset包括了相应的字符编码方案）；
  Accept-Encoding：浏览器申明自己接收的编码方法，通常指定压缩方法，是否支持压缩，支持什么压缩方法（gzip，deflate），（注意：这不是只字符编码）；
  Accept-Language：浏览器申明自己接收的语言。语言跟字符集的区别：中文是语言，中文有多种字符集，比如big5，gb2312，gbk等等；
  Content-Type：WEB服务器告诉浏览器自己响应的对象的类型和字符集。例如：Content-Type: text/html; charset='gb2312'
  Content-Encoding：WEB服务器表明自己使用了什么压缩方法（gzip，deflate）压缩响应中的对象。例如：Content-Encoding：gzip
  Content-Language：WEB服务器告诉浏览器自己响应的对象的语言。
  
  

  参考文献&进一步阅读

1. 百度百科. 字符集. http://baike.baidu.com/view/51987.htm, 2010-12-28
2. 维基百科. 字符编码. http://zh.wikipedia.org/wiki/%E5%AD%97%E7%AC%A6%E7%BC%96%E7%A0%81, 2011-1-5
3. 维基百科. ASCII. http://zh.wikipedia.org/wiki/ASCII, 2011-4-5
4. 维基百科. GB2312. http://zh.wikipedia.org/wiki/GB_2312, 2011-3-17
5. 维基百科. GB18030. http://zh.wikipedia.org/wiki/GB_18030, 2010-3-10
6. 维基百科. GBK. http://zh.wikipedia.org/wiki/GBK, 2011-3-7
7. 维基百科. Unicode. http://zh.wikipedia.org/wiki/Unicode, 2011-4-30
8. Laruence. 字符编码详解(基础). http://www.laruence.com/2009/08/22/1059.html, 2009-8-22
9. Jan Hunt. Character Sets and Encoding for Web Designers - UCS/UNICODE. http://www.uninetnews.com/other_standards/charset.php

一次谷歌面试趣事

本文原始地址：一次谷歌面试趣事

---

很多年前我进入硅谷人才市场，当时是想找一份高级工程师的职位。如果你有一段时间没有面试过，根据经验，有个非常有用的提醒你应该接受，就是：你往往会在前几次面试中的什么地方犯一些错误。简单而言就是，不要首先去你梦想的公司里面试。面试中有多如牛毛的应该注意的问题，你可能全部忘记了，所以，先去几个不太重要的公司里面试，它们会在这些方面对你起教育(再教育)作用。

我第一家面试的公司叫做gofish.com，据我所知，gofish这家公司如今的情况跟我当时面试时完全的不同。我几乎能打保票的说，当时我在那遇到的那些人都已不再那工作了，这家公司的实际情况跟我们这个故事并不是很相关。但在其中的面试却是十分相关的。对我进行技术性面试的人是一个叫做Guy的家伙。

Guy穿了一条皮裤子。众所周知，穿皮裤子的面试官通常是让人"格外"恐怖的。而Guy也没有任何让人失望的意思。他同样也是一个技术难题终结者。而且是一个穿皮裤子的技术难题终结者 —— 真的，我做不到他那样。

我永远不会忘记他问我的一个问题。事实上，这个问题是非常的普通 —— 在当时也是硅谷里标准的面试题。

问题是这样的：

假设这有一个各种字母组成的字符串，假设这还有另外一个字符串，而且这个字符串里的字母数相对少一些。从算法是讲，什么方法能最快的查出所有小字符串里的字母在大字符串里都有？

比如，如果是下面两个字符串：

String 1: ABCDEFGHLMNOPQRS

String 2: DCGSRQPOM

答案是true，所有在string2里的字母string1也都有。如果是下面两个字符串：

String 1: ABCDEFGHLMNOPQRS

String 2: DCGSRQPOZ

答案是false，因为第二个字符串里的Z字母不在第一个字符串里。

当他问题这个问题时，不夸张的说，我几乎要脱口而出。事实上，对这个问题我很有信心。(提示：我提供的答案对他来说显然是最糟糕的一种，从面试中他大量的各种细微表现中可以看出来)。

对于这种操作一种幼稚的做法是轮询第二个字符串里的每个字母，看它是否同在第一个字符串里。从算法上讲，这需要O(n*m)次操作，其中n是string1的长度，m是string2的长度。就拿上面的例子来说，最坏的情况下将会有16*8 = 128次操作。

一个稍微好一点的方案是先对这两个字符串的字母进行排序，然后同时对两个字串依次轮询。两个字串的排序需要(常规情况)O(m log m) + O(n log n)次操作，之后的线性扫描需要O(m+n)次操作。同样拿上面的字串做例子，将会需要16*4 + 8*3 = 88加上对两个字串线性扫描的16 + 8 = 24的操作。(随着字串长度的增长，你会发现这个算法的效果会越来越好)

最终，我告诉了他一个最佳的算法，只需要O(n+m)次操作。方法就是，对第一个字串进行轮询，把其中的每个字母都放入一个Hashtable里(成本是O(n)或16次操作)。然后轮询第二个字串，在Hashtable里查询每个字母，看能否找到。如果找不到，说明没有匹配成功。这将消耗掉8次操作 —— 这样两项操作加起来一共只有24次。不错吧，比前面两种方案都要好。

Guy没有被打动。他把他的皮裤子弄的沙沙响作为回应。"还有没有更好的？"他问道。

我的天？这个家伙究竟想要什么？我看看白板，然后转向他。"没有了，O(n+m)是你能得到的最好的结果了 —— 我是说，你至少要对每个字母至少访问一次才能完成这项操作 —— 而这个方案是刚好是对每个字母只访问一次"。我越想越确信我是对的。

他走到白板前，"如果这样呢 —— 假设我们有一个一定个数的字母组成字串 —— 我给每个字母分配一个素数，从2开始，往后类推。这样A将会是2，B将会是3，C将会是5，等等。现在我遍历第一个字串，把每个字母代表的素数相乘。你最终会得到一个很大的整数，对吧？然后 —— 轮询第二个字符串，用每个字母除它。如果除的结果有余数，这说明有不匹配的字母。如果整个过程中没有余数，你应该知道它是第一个字串恰好的子集了。这样不行吗？"

每当这个时候 —— 当某个人的奇思异想超出了你的思维模式时，你真的需要一段时间来跟上他的思路。现在他站在那里，他的皮裤子并没有帮助我理解他。

现在我想告诉你 —— Guy的方案(不消说，我并不认为Guy是第一个想出这招的人)在算法上并不能说就比我的好。而且在实际操作中，你很可能仍会使用我的方案，因为它更通用，无需跟麻烦的大型数字打交道。但从"巧妙水平"上讲，Guy提供的是一种更、更、更有趣的方案。

我没有得到这份职位。也许是因为我拒绝了他们提供给我的一些讨厌的工作内容和其它一些东西，但这都无所谓了。我还有更大更好的目标呢。

接着，我应聘了become.com。在跟CTO的电话面试中，他给我布置了一道"编程作业"。这个作业有点荒唐 —— 现在回想起来，大概用了我3天的时间去完成。我得到了面试，得到了那份工作 —— 但对于我来说，最大的收获是这道编程作业强迫我去钻研并有所获。我需要去开发一个网页爬虫，一个拼写检查/纠正器，还有一些其它的功能。不错的东西。然而，最终，我拒绝了这份工作。

终于，我来到了Google面试。我曾说过Google的面试过程跟外面宣传的很一致。冗长 —— 严格，但诚实的说，相当的公平。他们在各种面试过程中尽最大的努力去了解你、你的能力。并不是说他们在对你做科学研究，但我确信他们是努力这样做。

我在Google的第四场面试是一个女工程师，老实话，是一场很无聊的面试。在前面几场面试中我表现的很好，感觉到我的机会非常的大。我相信如果不做出什么荒唐事情来，十拿九稳我能得到这份工作。

她问了我一些关于排序或设计方面的非常简单的问题，我记不清了。但就在45分钟的面试快要结束时，她对我说"我还有一个问题。假设你有一个一定长度的由字母组成的字符串。你还有另外一个，短些。你如何才能知道所有的在较短的字符串里的字母在长字符串里也有？"

哇塞。Guy附身了。

现在，我完全可以马上结束这场面试。我可以对她说"哈哈，几个星期前我就知道答案啦！"，这是事实。但就是在几个星期前被问到这个问题时 —— 我给出的也是正确的答案。这是我本来就知道答案的问题。看起来就好像是Guy为我的这次面试温习过功课一样。而且，可恶，人们通常是通过上网来搜集面试问题 —— 而我，我可以毫不客气的说，对于这些问题，我不需要任何"作弊"。我自己知道这些答案！

现在你们可能认为——就在她问出了问题之后，在我准备开始说出在脑海里构思完成的最后的演讲之前——你们可能会想，我应该是，当然该，从情理上讲，镇定的回答出这个问题，并且获得赞赏。可糟糕的是，事实并不是这样。打个比喻，就像是她问出来问题后，我在闹子里立即举起了手，并大叫着"我！嗨！嗨！我知道！让我来回答吧！"我的大脑试图夺走我对嘴巴的控制权(这事经常发生)，幸亏我坚强的毅力让我镇定下来。

于是我开始回答。平静的。带着不可思议的沉着和优雅。带着一种故意表现出来的 —— 带着一种，我认为，只有那种完全的渊博到对古今中外、不分巨细的知识都精通的人才能表现出来的自信。

我轻描淡写的说出来那种很幼稚的方案，就好象是这种方案毫无价值。我提到了给它们排序，就好像是在给早期的《星际迷航》中的一个场景中的人物穿上红T恤似的。最后，平淡的，就好像是我决定了所有事情的好坏、算法上的效率，我说出了O(n+m)一次性方案。

我要告诉你——尽管我表明上的平静——这整个过程我却在做激烈的挣扎，内心里我在对自己尖着——"你个笨蛋，赶紧告诉她素数方案！"

当我完成了对一次性算法的解释后，她完全不出意外的认可的点了下头，并开始在笔记本上记录。这个问题她以前也许问过了一百次，我想大部分的人都能回答上来。她也许写的是"回答正确。无聊的面试。正确的回答了无聊的字符串问题。没有惊喜。无聊的家伙，但可以留下。"

我等了一会。我让这种焦灼的状态持续的尽可能的长。我可以发誓的说，如果再耽搁一分钟，我一定会憋出脑血栓、脱口说出关于素数的未解之谜。

我打破了沉默。"你知道吗，还有另外一个，可能是更聪明的算法。"

她二目空空的抬头看了一眼，仅在瞬间闪现过一丝希望。

"假设我们有一定长度的字符串。我们可以给每个字母分配一个素数，从2开始。然后我们把大字串中的每个字母代表的素数相乘得出一个数，用小字串中的每个字母代表的素数去除它。如果除的过程中没有产生余数，则小字串是大字串的一个子集。"

在此时，我猜，她看起来就像是Guy当时把相同的话说给我听时我表现出来的样子。而我演讲时泰然自若的表情没了，眼睛瞪大，说话时稍微带出来一些唾沫星子。

一会儿后，她不得不说了，"可是…等一下，有可能…是的，可以这样！可是如何…如果…噢，噢，可行！简洁！"

我得意洋洋的吸了一口气。我在我的面试记录里写下了"她给了我一个'简洁'的评语！"在她提出这个问题之前我就确信能得到这份工作，现在我更加确信了。还有一点我十分确信的是，我(更准确的说是Guy)给了她今天的好心情。

我在Google干了3年，生活的十分愉快。我在2008年辞职去到一个小公司里做CTO，之后又开办了一个自己的公司。大概是一年前，我偶然的在一个创业论坛会上遇到了Guy，他记不得我了，当我向他细述这段往事时，他对他那条皮裤子大笑不已。

话说回来，如果这个故事里有什么教育意义的话——永远不要冒失的首先去应聘你梦想的公司，应先去应聘那些你不看好的职位。你除了能从这些面试中获得经验外，你指不定能遇到某个能为你的更重要的面试铺路的人呢。事实上，这个经验在你生活中的很多其它事情上也适应。

说正经的，如果你有机会想找一个解决问题的高手——雇佣Guy比谁都强。那个家伙很厉害。

(在这些陈年旧账里发现的一点技术瑕疵：字母有可能重复而字符串可能会很长，所以必须要有统计。用那个最幼稚的解决方案时，当在大字符串里找到一个字符后就把它删掉，当这样仍然是 O(n*m)次。在Hashtable里我们会有一个key->value的计数。Guy的方案在这种情况下仍然好用。)

修改：11/30/10 —— 本文中提到的Guy看到了这篇文章，并在评论中做了澄清。值得一读。

---

如何计算某一天是星期几?—— 蔡勒（Zeller）公式

来源:原文地址

---

历史上的某一天是星期几？未来的某一天是星期几？关于这个问题，有很多计算公式（两个通用计算公式和一些分段计算公式），其中最著名的是蔡勒（Zeller）公式。即w=y+[y/4]+[c/4]-2c+[26(m+1)/10]+d-1



公式中的符号含义如下，w：星期；c：世纪-1；y：年（两位数）；m：月（m大于等于3，小于等于14，即在蔡勒公式中，某年的1、2月要看作上一年的13、14月来计算，比如2003年1月1日要看作2002年的13月1日来计算）；d：日；[ ]代表取整，即只要整数部分。(C是世纪数减一，y是年份后两位，M是月份，d是日数。1月和2月要按上一年的13月和 14月来算，这时C和y均按上一年取值。)算出来的W除以7，余数是几就是星期几。如果余数是0，则为星期日。



以2049年10月1日（100周年国庆）为例，用蔡勒（Zeller）公式进行计算，过程如下：

蔡勒（Zeller）公式：w=y+[y/4]+[c/4]-2c+[26(m+1)/10]+d-1

=49+[49/4]+[20/4]-2×20+[26× (10+1)/10]+1-1

=49+[12.25]+5-40+[28.6]

=49+12+5-40+28

=54 (除以7余5)

即2049年10月1日（100周年国庆）是星期5。



你的生日（出生时、今年、明年）是星期几？不妨试一试。



不过，以上公式只适合于1582年10月15日之后的情形（当时的罗马教皇将恺撒大帝制订的儒略历修改成格里历，即今天使用的公历）。过程的推导:(对推理不感兴趣的可略过不看)

星期制度是一种有古老传统的制度。据说因为《圣经·创世纪》中规定上帝用了六天时间创世纪，第七天休息，所以人们也就以七天为一个周期来安排自己的工作和生活，而星期日是休息日。从实际的角度来讲，以七天为一个周期，长短也比较合适。所以尽管中国的传统工作周期是十天（比如王勃《滕王阁序》中说的“十旬休暇”，即是指官员的工作每十日为一个周期，第十日休假），但后来也采取了西方的星期制度。



在日常生活中，我们常常遇到要知道某一天是星期几的问题。有时候，我们还想知道历史上某一天是星期几。通常，解决这个方法的有效办法是看日历，但是我们总不会随时随身带着日历，更不可能随时随身带着几千年的万年历。假如是想在计算机编程中计算某一天是星期几，预先把一本万年历存进去就更不现实了。这时候是不是有办法通过什么公式，从年月日推出这一天是星期几呢？



答案是肯定的。其实我们也常常在这样做。我们先举一个简单的例子。比如，知道了2004年5月1日是星期六，那么2004年5月31日“世界无烟日”是星期几就不难推算出来。我们可以掰着指头从1日数到31日，同时数星期，最后可以数出5月31日是星期一。其实运用数学计算，可以不用掰指头。我们知道星期是七天一轮回的，所以5月1日是星期六，七天之后的5月8日也是星期六。在日期上，8-1=7，正是7的倍数。同样，5月15日、5月22日和5月29日也是星期六，它们的日期和5月1日的差值分别是14、21和28，也都是7的倍数。那么5月31日呢？31-1=30，虽然不是7的倍数，但是31除以7，余数为2，这就是说，5月31日的星期，是在5月1日的星期之后两天。星期六之后两天正是星期一。



这个简单的计算告诉我们计算星期的一个基本思路：首先，先要知道在想算的日子之前的一个确定的日子是星期几，拿这一天做为推算的标准，也就是相当于一个计算的“原点”。其次，知道想算的日子和这个确定的日子之间相差多少天，用7除这个日期的差值，余数就表示想算的日子的星期在确定的日子的星期之后多少天。如果余数是0，就表示这两天的星期相同。显然，如果把这个作为“原点”的日子选为星期日，那么余数正好就等于星期几，这样计算就更方便了。



但是直接计算两天之间的天数，还是不免繁琐。比如1982年7月29日和2004年5月1日之间相隔7947天，就不是一下子能算出来的。它包括三段时间：一，1982年7月29日以后这一年的剩余天数；二，1983-2003这二十一个整年的全部天数；三，从2004年

元旦到5月1日经过的天数。第二段比较好算，它等于21*365+5=7670天，之所以要加5，是因为这段时间内有5个闰年。第一段和第三段就比较麻烦了，比如第三段，需要把5月之前的四个月的天数累加起来，再加上日期值，即31+29+31+30+1=122天。同理，第一段需要把7月之后的五个月的天数累加起来，再加上7月剩下的天数，一共是155天。所以总共的相隔天数是122+7670+155=7947天。



仔细想想，如果把“原点”日子的日期选为12月31日，那么第一段时间也就是一个整年，这样一来，第一段时间和第二段时间就可以合并计算，整年的总数正好相当于两个日子的年份差值减一。如果进一步把“原点”日子选为公元前1年12月31日（或者天文学家所使用的公元0年12月31日），这个整年的总数就正好是想算的日子的年份减一。这样简化之后，就只须计算两段时间：一，这么多整年的总天数；二，想算的日子是这一年的第几天。巧的是，按照公历的年月设置，这样反推回去，公元前1年12月31日正好是

星期日，也就是说，这样算出来的总天数除以7的余数正好是星期几。那么现在的问题就只有一个：这么多整年里面有多少闰年。这就需要了解公历的置闰规则了。



我们知道，公历的平年是365天，闰年是366天。置闰的方法是能被4整除的年份在2月加一天，但能被100整除的不闰，能被400整除的又闰。因此，像1600、2000、2400年都是闰年，而1700、1800、1900、2100年都是平年。公元前1年，按公历也是闰年。



因此，对于从公元前1年（或公元0年）12月31日到某一日子的年份Y之间的所有整年中的闰年数，就等于



[(Y-1)/4] - [(Y-1)/100] + [(Y-1)/400]，



[...]表示只取整数部分。第一项表示需要加上被4整除的年份数，第二项表示需要去掉被100整除的年份数，第三项表示需要再加上被400整除的年份数。之所以Y要减一，这样，我们就得到了第一个计算某一天是星期几的公式：



W = (Y-1)*365 + [(Y-1)/4] - [(Y-1)/100] + [(Y-1)/400] + D．              (1)



其中D是这个日子在这一年中的累积天数。算出来的W就是公元前1年（或公元0年）12月31日到这一天之间的间隔日数。把W用7除，余数是几，这一天就是星期几。比如我们来算2004年5月1日：



W = (2004-1)*365 + [(2004-1)/4] - [(2004-1)/100] + [(2004-1)/400] +

   (31+29+31+30+1)

  = 731702，



731702 / 7 = 104528……6，余数为六，说明这一天是星期六。这和事实是符合的。



上面的公式(1)虽然很准确，但是计算出来的数字太大了，使用起来很不方便。仔细想想，其实这个间隔天数W的用数仅仅是为了得到它除以7之后的余数。这启发我们是不是可以简化这个W值，只要找一个和它余数相同的较小的数来代替，用数论上的术语

来说，就是找一个和它同余的较小的正整数，照样可以计算出准确的星期数。



显然，W这么大的原因是因为公式中的第一项(Y-1)*365太大了。其实，



(Y-1)*365 = (Y-1) * (364+1)

          = (Y-1) * (7*52+1)

          = 52 * (Y-1) * 7 + (Y-1)，



这个结果的第一项是一个7的倍数，除以7余数为0，因此(Y-1)*365除以7的余数其实就等于Y-1除以7的余数。这个关系可以表示为：



(Y-1)*365 ≡ Y-1 (mod 7)．



其中，≡是数论中表示同余的符号，mod 7的意思是指在用7作模数（也就是除数）的情况下≡号两边的数是同余的。因此，完全可以用(Y-1)代替(Y-1)*365，这样我们就得到了那个著名的、也是最常见到的计算星期几的公式：



W = (Y-1) + [(Y-1)/4] - [(Y-1)/100] + [(Y-1)/400] + D．                  (2)



这个公式虽然好用多了，但还不是最好用的公式，因为累积天数D的计算也比较麻烦。是不是可以用月份数和日期直接计算呢？答案也是肯定的。我们不妨来观察一下各个月的日数，列表如下：



月　　份：1月　2月　　3月　4月　5月　6月　7月　8月　9月　10月　11月　12月

--------------------------------------------------------------------------

天　　数： 31  28(29)  31   30   31   30   31   31   30   31    30    31



如果把这个天数都减去28（=4*7），不影响W除以7的余数值。这样我们就得到另一张表：



月　　份：1月　2月　3月　4月　5月　6月　7月　8月　9月　10月　11月　12月

------------------------------------------------------------------------

剩余天数： 3   0(1)  3    2    3    2    3    3    2    3     2     3

平年累积： 3   3     6    8   11   13   16   19   21   24    26    29

闰年累积： 3   4     7    9   12   14   17   20   22   25    27    30



仔细观察的话，我们会发现除去1月和2月，3月到7月这五个月的剩余天数值是3,2,3,2,3；8月到12月这五个月的天数值也是3,2,3,2,3，正好是一个重复。相应的累积天数中，后一月的累积天数和前一月的累积天数之差减去28就是这个重复。正是因为这种规律的存在，平年和闰年的累积天数可以用数学公式很方便地表达：



    ╭ d；　　　　　　　　　　　　　　　 　（当M＝1）

D = {  31 + d；　　　　　　　　　    　　  （当M＝2） 　　　　　　　　　 (3)

    ╰ [ 13 * (M+1) / 5 ] - 7 + (M-1) * 28 + d + i．　 （当M≥3）



其中[...]仍表示只取整数部分；M和d分别是想算的日子的月份和日数；平年i=0，闰年i=1。对于M≥3的表达式需要说明一下：[13*(M+1)/5]-7算出来的就是上面第二个表中的平年累积值，再加上(M-1)*28就是想算的日子的月份之前的所有月份的总天数。这是一个很巧妙的办法，利用取整运算来实现3,2,3,2,3的循环。比如，对2004年5月1日，有：



D = [ 13 * (5+1) / 5 ] - 7 + (5-1) * 28 + 1 + 1

  = 122，



这正是5月1日在2004年的累积天数。



假如，我们再变通一下，把1月和2月当成是上一年的“13月”和“14月”，不仅仍然符合这个公式，而且因为这样一来，闰日成了上一“年”（一共有14个月）的最后一天，成了d的一部分，于是平闰年的影响也去掉了，公式就简化成：



D = [ 13 * (M+1) / 5 ] - 7 + (M-1) * 28 + d．        （3≤M≤14）        (4)



上面计算星期几的公式，也就可以进一步简化成：



W = (Y-1) + [(Y-1)/4] - [(Y-1)/100] + [(Y-1)/400] + [ 13 * (M+1) / 5 ] - 7

   + (M-1) * 28 + d．



因为其中的-7和(M-1)*28两项都可以被7整除，所以去掉这两项，W除以7的余数不变，公式变成：



W = (Y-1) + [(Y-1)/4] - [(Y-1)/100] + [(Y-1)/400] + [ 13 * (M+1) / 5 ] + d．

(5)



当然，要注意1月和2月已经被当成了上一年的13月和14月，因此在计算1月和2月的日子的星期时，除了M要按13或14算，年份Y也要减一。比如，2004年1月1日是星期四，用这个公式来算，有：



W = (2003-1) + [(2003-1)/4] - [(2003-1)/100] + [(2003-1)/400] + [13*(13+1)/5]

   + 1

  = 2002 + 500 - 20 + 5 + 36 + 1

  = 2524；

2524 / 7 = 360……4．这和实际是一致的。



公式(5)已经是从年、月、日来算星期几的公式了，但它还不是最简练的，对于年份的处理还有改进的方法。我们先来用这个公式算出每个世纪第一年3月1日的星期，列表如下：



年份：  1(401,801,…,2001)                   101(501,901,…,2101)

--------------------------------------------------------------------

星期：　4                                      2

====================================================================

年份：201(601,1001,…,2201)                  301(701,1101,…,2301)

--------------------------------------------------------------------

星期：  0                                      5



可以看出，每隔四个世纪，这个星期就重复一次。假如我们把301(701,1101,…,2301)年3月1日的星期数看成是-2（按数论中对余数的定义，-2和5除以7的余数相同，所以可以做这样的变换），那么这个重复序列正好就是一个4,2,0,-2的等差数列。据此，我们可以得到下面的计算每个世纪第一年3月1日的星期的公式：



W = (4 - C mod 4) * 2 - 4．                                              (6)



式中，C是该世纪的世纪数减一，mod表示取模运算，即求余数。比如，对于2001年3月1日，C=20，则：



W = (4 - 20 mod 4) * 2 - 4

  = 8 - 4

  = 4．



把公式(6)代入公式(5)，经过变换，可得：



(Y-1) + [(Y-1)/4] - [(Y-1)/100] + [(Y-1)/400] ≡ (4 - C mod 4) * 2 - 1

(mod 7)．                                                               (7)



因此，公式(5)中的(Y-1) + [(Y-1)/4] - [(Y-1)/100] + [(Y-1)/400]这四项，在计算每个世纪第一年的日期的星期时，可以用(4 - C mod 4) * 2 - 1来代替。这个公式写出来就是：



W = (4 - C mod 4) * 2 - 1 + [13 * (M+1) / 5] + d．                       (8)



有了计算每个世纪第一年的日期星期的公式，计算这个世纪其他各年的日期星期的公式就很容易得到了。因为在一个世纪里，末尾为00的年份是最后一年，因此就用不着再考虑“一百年不闰，四百年又闰”的规则，只须考虑“四年一闰”的规则。仿照由公式(1)

简化为公式(2)的方法，我们很容易就可以从式(8)得到一个比公式(5)更简单的计算任意

一天是星期几的公式：



W = (4 - C mod 4) * 2 - 1 + (y-1) + [y/4] + [13 * (M+1) / 5] + d．       (9)



式中，y是年份的后两位数字。



如果再考虑到取模运算不是四则运算，我们还可以把(4 - C mod 4) * 2进一步改写成只含四则运算的表达式。因为世纪数减一C除以4的商数q和余数r之间有如下关系：



4q + r = C，



其中r即是 C mod 4，因此，有：



r = C - 4q

  = C - 4 * [C/4]．                                                     (10)



则



(4 - C mod 4) * 2 ＝ (4 - C + 4 * [C/4]) * 2

                  ＝ 8 - 2C + 8 * [C/4]

                  ≡ [C/4] - 2C + 1 (mod 7)．                           (11)



把式(11)代入(9)，得到：



W = [C/4] - 2C + y + [y/4] + [13 * (M+1) / 5] + d - 1．                 (12)



这个公式由世纪数减一、年份末两位、月份和日数即可算出W，再除以7，得到的余数是几就表示这一天是星期几，唯一需要变通的是要把1月和2月当成上一年的13月和14月，C和y都按上一年的年份取值。因此，人们普遍认为这是计算任意一天是星期几的最好的公式。这个公式最早是由德国数学家克里斯蒂安·蔡勒（Christian Zeller, 1822-1899）在1886年推导出的，因此通称为蔡勒公式（Zeller’s Formula）。为方便口算，式中的[13 * (M+1) / 5]也往往写成[26 * (M+1) / 10]。



现在仍然让我们来算2004年5月1日的星期，显然C=20，y=4，M=5，d=1，代入蔡勒公式，有：



W = [20/4] - 40 + 4 + 1 + [13 * (5+1) / 5] + 1 - 1

  = -15．



注意负数不能按习惯的余数的概念求余数，只能按数论中的余数的定义求余。为了方便计算，我们可以给它加上一个7的整数倍，使它变为一个正数，比如加上70，得到55。再除以7，余6，说明这一天是星期六。这和实际是一致的，也和公式(2)计算所得的结果一致。



最后需要说明的是，上面的公式都是基于公历（格里高利历）的置闰规则来考虑的。对于儒略历，蔡勒也推出了相应的公式是：



W = 5 - C + y + [y/4] + [13 * (M+1) / 5] + d - 1．                      (13)



这样，我们终于一劳永逸地解决了不查日历计算任何一天是星期几的问题。

x&(x-1)

来源： 原文链接

---

昨天在淘宝招聘会上遇到的这道笔试题：求下面函数的返回值 -- 统计1的个数

int func(int x)
{
    int countx = 0;
    while(x)
    {
        countx++;
        x = x&(x-1);
    }
    return countx;
}

假定x = 9999
10011100001111
答案: 8

思路: 将x转化为2进制，看含有的1的个数。
注: 每执行一次x = x&(x-1)，会将x用二进制表示时最右边的一个1 变为0，因为x-1将会将该位(x用二进制表示时最右边的一个1)变为0。

判断一个数(x)是否是2的n次方
-------------------------------------

#include <stdio.h>

int func(int x)
{
    if( (x&(x-1)) == 0 )
        return 1;
    else
        return 0;
}

int main()
{
    int x = 8;
    printf("%d\n", func(x));
}

注:
(1) 如果一个数是2的n次方，那么这个数用二进制表示时其最高位为1，其余位为0。
(2) ==优先级高于&

运行级别及Ubuntu启动进入文本模式

Update 20111028 以前转载的内容可能只适用于某个版本（至少Ubuntu 9.10就不适用了），又找到一些方法，经试用可行，记录在此。 来源：ubuntu 开机启动终端 字符模式 文本模式 注意　debian类系统的启动级别和往常的redhat等不同 rc0表示关机rc6表示重启 rc1表示单用户模式 rc2-rc4表示多用户模式 （ 0　关机 1　单用户模式 2　不带网络的多用户模式 3　带网络的多用户，也就是所谓的纯字符模式 4　保留，用户可以自给定义 5　图形界面的多用户模式 6　重起系统 ） 所以如果你想要启动到终端的话 你只需要关闭gdm的服务 我介绍一个简单的方法 代码: sudo apt-get install sysv-rc-conf sudo sysv-rc-conf 然后在里面找到一个叫做gdm的服务，别且在所有级别关闭它 然后q就ok了 找到的第二种方法 用nano编辑 /etc/X11/default-display-manager,把/usr/sbin/gdm注释掉,即在前面加个#号,改成#/usr/sbin/gdm,然后在加一行false这样保存既可. 完整的是这样： #/usr/sbin/gdm false 修改后重启，这样启动就是字符界面了。 找到的第三种方法 # 0 - halt (Do NOT set initdefault to this) 关机(不要设置为默认) # 1 - Single user mode 单用户模式 # 2 - Multiuser, without NFS (The same as 3, if you do not have networking) 多用户模式，但不支持NFS # 3 - Full multiuser mode 完全的多用户模式 # 4 - unused 没用到 # 5 - X11 图形界面 # 6 - reboot (Do NOT set initdefault to this) 重启(不要设置为默认) RedHat中要改变启动级别，只要修改/etc/inittab。Ubuntu有点不一样，网上的方法也很多，试过其中一种。 　　You need to open the /etc/default/grub file, locate the following line: 　　GRUB_CMDLINE_LINUX_DEFAULT="quiet splash" 　　and change it to: 　　GRUB_CMDLINE_LINUX_DEFAULT="quiet splash text" 　　update-grub 即编辑/etc/default/grub文件，将GRUB_CMDLINE_LINUX_DEFAULT="quiet splash"改为GRUB_CMDLINE_LINUX_DEFAULT="quiet splash text"，然后更新一下grub。 方法三还可以。如果想用这种方法永远启动到字符终端模式，则可以修改/boot/grub/grub.cfg，在相应的位置添加txt参照即可。但是grub.cfg是 自动生成的，所有的在里面的修改都可能被其它的操作覆盖掉，比如update-grub命令，如果不想被覆盖，则修改/etc/default/grub 把 GRUB_CMDLINE_LINUX_DEFAULT="quiet splash" GRUB_CMDLINE_LINUX="" 改成 GRUB_CMDLINE_LINUX_DEFAULT="text" GRUB_CMDLINE_LINUX="" 然后再运行一下update-grub命令，它会自动添加上text参数到内核参数中。 说明： 1，无论使用什么方式启动到字符终端模式，你都可以使用命令startx命令来启动Xwindow 2，在10.04 lucid 下测试成功 参数的含义（个人猜测，没有在网上找到相关内容） quiet 阻止内核输入到命令行 splash 显示启动画面，如ubuntu logo text 启动到字符终端模式 我的同时写上quiet 和text就起不来，停在checking battery status 下面不动了，也可以我为了测试等待的时间不够长，虽然不动了，可以按CTRL+ALT+DELETE重新启动。 文本与桌面模式切换： 文本模式登陆后，在普通用户权限下执行startx，进入到桌面模式。 一定要在普通用户权限下，root权限下startx，桌面模式都是默认设置，不加载个人设置！ 桌面到文本的切换： Ctrl+Alt+F1，切到文本界面，执行Ctrl+c，结束掉刚才启动的X server！

---

以下为旧文 来源：未知 Linux系统有7个运行级别(runlevel)  (注意下文，debian系衍生的linux 运行级不一样) 运行级别0：系统停机状态，系统默认运行级别不能设为0，否则不能正常启动 运行级别1：单用户工作状态，root权限，用于系统维护，禁止远程登陆 运行级别2：多用户状态(没有NFS) 运行级别3：完全的多用户状态(有NFS)，登陆后进入控制台命令行模式 运行级别4：系统未使用，保留 运行级别5：X11控制台，登陆后进入图形GUI模式 运行级别6：系统正常关闭并重启，默认运行级别不能设为6，否则不能正常启动 运行级别的原理： 1。在目录/etc/rc.d/init.d下有许多服务器脚本程序，一般称为服务(service) 2。在/etc/rc.d下有7个名为rcN.d的目录，对应系统的7个运行级别 3。rcN.d目录下都是一些符号链接文件，这些链接文件都指向init.d目录下的service脚本文件，命名规则为K+nn+服务名或S+nn+服务名，其中nn为两位数字。 4。系统会根据指定的运行级别进入对应的rcN.d目录，并按照文件名顺序检索目录下的链接文件      对于以K开头的文件，系统将终止对应的服务      对于以S开头的文件，系统将启动对应的服务 5。查看运行级别用：runlevel 6。进入其它运行级别用：init N 7。另外init0为关机，init 6为重启系统 ____________________________________________________________________________________________ 因为debian 系衍生出来的linux 一向是没有使用/etc/inittab 作为登入状态文档来使用的。但是虽然没有系统默认没有这个文件，但是你可以自己建一个inittab文件。 因为从/etc/event.d/中的rc-default文件中代码可以看出： script runlevel --reboot || true if grep -q -w -- "-s\|single\|S" /proc/cmdline; then telinit S elif [ -r /etc/inittab ]; then RL="$(sed -n -e "/^id:[0-9]*:initdefault:/{s/^id://;s/:.*//;p}" /etc/inittab || true)" if [ -n "$RL" ]; then telinit $RL else telinit 2 fi else telinit 2 fi end script 系统会首先搜寻inittab文件，如果不存在，那么将运行在2级别上。所以你可以自己建个inittab文件，或者把相应的telinit 2 改为 telinit X（你想要运行的级别） 转到kubuntu之前曾经学习了一下，了解到ubuntu在6.10开始用upstart替代init，主要脚本都在/etc/event.d下面，默认情况下/etc下没有inittab文件。 刚装上kubuntu时候专门到/etc/event.d下看了一下，特别注意到rc-default这个脚本，里面有一段内容: elif [ -r /etc/inittab ] then 说明默认情况下inittab虽然不存在，但是用户建立的inittab还是会被注意到的。然后又经别人的指点看了一下/usr/share/doc/upstart/下面的文档，其中README.Debian中有这么一段内容： 这就给我这样一个印象，即虽然ubuntu用upstart替代init，但还是和init保持兼容。 今天正好需要将系统直接启动到字符界面下，即不启动kdm。 edit the /etc/inittab file 那就试试自建一个inittab文件，并按照以前的习惯写入一行id:3:initdefault: ，保存后重新启动，结果发现毫无变化，依然启动到桌面，有点纳闷，难道inittab不起作用？在终端里输入runlevel检查当前状态，显示 N 3，说明inittab有效果，那是什么原因呢？ 将刚才建立的inittab移除，将系统恢复到之前的状态并重新启动，再用runlevel检查，显示 N 2，说明ubuntu系统的default runlevel可能是2，这和我以前的常识有些冲突，看来又需要学习了。 先去分别查看/etc/rc2.d至rc5.d下的内容，发现基本一致，都启动了kdm。这与其他的linux发行版不太一致，通常runlevel 3是Multi user mode，即直接登录到字符界面；而runlevel 5是Multi user mode with GUI，即登录到图形界面。 后来在Debian的FAQ里面搜索到这样的内容： 0(halt the system) 1(single-user mode) 2through5(various muli-user modes),and 6(reboot the system) 小区别就在这里了，看来debian以及衍生出来的发行版，如ubuntu的default runlevel确实是2，而且id 2至5都是一样的。 真相大白，再次建立inittab，写入id:3:initdefault: ，然后进入/etc/rc3.d，重命名S30gdm，重新启动系统，如愿以偿进入字符界面。 

在VC9.0中实现C++模板类头文件和实现文件分离的方法

来源：原文链接

---

如何实现C++模板类头文件和实现文件分离，这个问题和编译器有关。

引用<>里的观点：1）标准C++为编译模板代码定义了两种模型：“包含”模型和“分别编译”模型。2）所有编译器都支持“包含”模型

，某些编译器支持“分别编译”模型。

问题的提出：（帖子在：http://topic.csdn.net/u/20101215/15/f4f270f2-f0f9-4c5f-8765-1bfde2aeebbf.html）

第一种方法：按C++primer中的“包含”模型，在定义模板类的头文件中的末行用语句：#include "template_compile.cpp"

在类模板头文件template_compile.h中：


template  
class base
{
public:
    base() {};
    ~base() {};
    T add_base(T x,T y);
};
#include "template_compile.cpp"


在类模板的实现文件template_compile.cpp中：


template  
T base::add_base(T x,T y)  
{
    return x+y;
}


在使用模板的测试文件use_template.cpp中：

#include  
#include "template_compile.h"
using namespace std;
void main()
{
...
}


这种方法不能通过编译，"template_compile.cpp"文件不能"看见"“template_compile.h"文件。

然而：如果我把类模板的实现文件里代码放在类模板的头文件中，注释掉：#include "template_compile.cpp"，编译和运行不会有任何错误。理论上”把类模

板的实现文件里代码放在类模板的头文件中“和”在定义模板类的头文件中的末行用语句：#include "template_compile.cpp" “是一致的，但编译器就是通不

过。

实验证明：VC9.0不支持C++primer中所说的“包含”模型。

第二种方法：bruceteen提出的：使用define

在类模板头文件template_compile.h中：


template  
class base
{
public:
  base() {};
  ~base() {};
  T add_base(T x,T y);
};
#define xxx
#include "template_compile.cpp"


在类模板的实现文件template_compile.cpp中：


#ifdef xxx
template  
T base::add_base(T x,T y)  
{
  return x+y;
}
#endif


测试文件不变。

实验证明：在VC9.0中，这种方法可以实现类模板头文件和实现文件的分离

方法三：

在类模板头文件template_compile.h中：


template  
class base
{
public:
    base() {};
    ~base() {};
    T add_base(T x,T y);
};


在类模板的实现文件template_compile.cpp中：


#include "template_compile.h"
template  
T base::add_base(T x,T y)  
{
    return x+y;
}


在使用模板的测试文件use_template.cpp中：使用#include "template_compile.cpp"


#include  
#include "template_compile.cpp"
using namespace std;
void main()
{
...
}


实验证明：在VC9.0中，这种方法可以实现类模板头文件和实现文件的分离。

另外实验证明：VC9.0不支持“分别编译”模型。

“火柴棍式”程序员面试题

来源：原文链接

---

有时候，有些面试题是很是无厘头，这不，又有一个，还记得小时候玩的的"火柴棍游戏"吗，就是移动一根火柴棍改变一个图或字的游戏。程序面试居然也可以这么玩，看看下面这个火柴棍式的程序面试题吧。

下面是一个C程序，其想要输出20个减号，不过，粗心的程序员把代码写错了，你需要把下面的代码修改正确，不过，你只能增加或是修改其中的一个字符，请你给出三种答案。


int n = 20;
for(int i = 0; i < n; i--){
printf("-"); }


不要以为这题不是很难，我相信你并不那么容易能找到3种方法。我觉得，如果你能在10分钟内找出这三种方法，说明你真的很聪明，而且反应很快。当然，15分钟内也不赖。不过，你要是30分钟内找不到三种方法，当然，不说明你笨了，最多就是你的反应还不够快。嘿嘿。就当是玩玩吧。

下面是我的答案：

 
//第一种解法：在for循环中给n加一个负号 
for(int i = 0; i < -n; i--)  
//第二种解法：把 n 初始化成 -20 
int n = -20;  
//第三种解法：把for循环中的 i 初始化成40 
for(int i = 40; i < n; i--) 

不过，我要告诉你，以上这些答案都不对（我就知道你会偷看答案的），不过，顺着这些思路走很接近了。呵呵。

下面是正确答案——

//第一种解法：在for循环中给 i 加一个负号
for(int i = 0; -i < n; i--)

//第二种解法：在for循环中把 i-- 变成 n--
for(int i = 0; i < n; n--)

//第三种解法：把for循环中的 < 变成 +
for(int i = 0; i + n; i--)

其它相关的变种题如下：

• 通过修改、增加一个字符，让其输出21个减号
• 通过修改、增加一个字符，让其只输出1个减号
• 通过修改、增加一个字符，让其不输出减号

（全文完）